Cauchy-Schwarz Inequality: Simple Definition, Example & Proof

Statistics Definitions > Cauchy-Schwarz Inequality

What is the Cauchy-Schwarz Inequality?

The Cauchy-Schwarz Inequality (also called Cauchy’s Inequality, the Cauchy-Bunyakovsky-Schwarz Inequality and Schwarz’s Inequality) is useful for bounding expected values that are difficult to calculate. It allows you to split E[X₁, X₂] into an upper bound with two parts, one for each random variable (Mukhopadhyay, 2000, p.149).

The formula is:



Given that X and Y have finite variances.

What this is basically saying is that for two random variables, X and Y, the expected value of the square of them multiplied together E(XY)² will always be less than or equal to the expected value of the product of the squares of each. E(X²)E(Y²).

Other Versions

The Cauchy-Schwarz inequality was developed by many people over a long period of time. It made its first appearance in Cauchy’s 1821 work Cours d’analyse de l’Ecole Royal Polytechnique and was further developed by Bunyakovsky (1859) and Schwarz (1888). As well as the different names, it can also be expressed in several different ways. For example, the inequality can be written, equivalently, as:
Cov²(X, Y) ≤ σ²_x σ²_y.

There is another version of the inequality that replaces the expectation E with time integrals. The formula is the same, with the exception of the expectation/integral replacement:

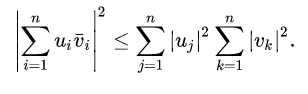
Applications

The Cauchy-Schwarz inequality is arguably the inequality with the widest number of applications. As well as probability and statistics, the inequality is used in many other branches of mathematics, including:

• Classical Real and Complex Analysis,
• Hilbert spaces theory,
• Numerical analysis,
• Qualitative theory of differential equations.

Example

Example question: use the Cauchy-Schwarz inequality to find the maximum of x + 2y + 3z,
given that x² + y² + z² = 1.

We know that: (x + 2y + 3x)² ≤ (1² + 2² 3²)(x² + y² + z²) = 14.

Therefore: x + 2y + 3z ≤ √14.

The equality holds when: x/1 = y/2 = z/3.

We are given that: x² + y² + z² = 1,
so:
x = 1/√14, x = 2/√14, x = 3/√14,

Proofs

This is one of the simplest proofs to visualize. The following “proof without words” is from Nelson (1994):



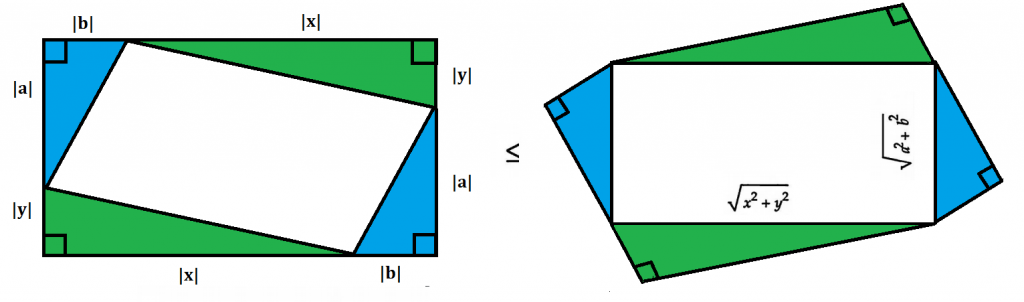
Here’s another proof, this time, in words:

Assume that E[X²]>0 and E[Y²]>0, and:

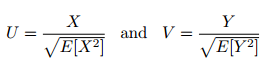
It can be shown that: 2|UV| ≤ U² + V².

Therefore: 2|E[UV] | ≤ 2E[|UV|] ≤ E[U²] + E[V²] = 2
Giving:
(E[UV])² ≤ (E[|UV|])² ≤ 1.

This implies that:



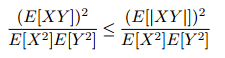
You can find a comprehensive list of proofs (12 in all!) for the Cauchy-Schwarz inequality in Win & Wu’s paper (PDF).

References

Bunyakovsky (1859). Inequalities, in Mémoires de l’Académie impériale des sciences de St. Pétersbourg. Retrieved January 7, 2018 from: https://www.biodiversitylibrary.org/bibliography/96968#/details.
Cauchy, A. (1821). Cours d’analyse de l’École royale polytechnique. Retrieved January 7, 2018 from: https://archive.org/details/coursdanalysede00caucgoog
Mukhopadhyay, N. (2000). Probability and Statistical Inference. CRC Press.
Nelsen, R. (1994). Proof without words: Cauchy-Schwarz inequality, Math. Mag., 67, no. 1, p. 20. Retrieved January 7, 2018 from: https://is.muni.cz/el/1441/podzim2013/MA2MP_SMR2/um/Nelsen–Proofs_without_Words.pdf
Schwarz, K. (1888). Uber ein die fl¨achen kleinsten fl¨acheninhalts betreffendes problem der variationsrechnung. Retrieved January 7, 2018 from: https://link.springer.com/chapter/10.1007%2F978-3-642-50665-9_11
Win, H. & Wu, S. (2000). Various proofs of the Cauchy-Schwarz inequality. Retrieved January 1, 2018 from: http://www.ajmaa.org/RGMIA/papers/v12e/Cauchy-Schwarzinequality.pdf