Probability Distributions > Burr Distribution
What is the Burr Distribution?
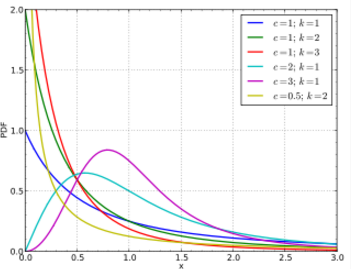
From crop prices to risk, the Burr distribution is widely used in modeling phenomena from a wide variety of fields. With its diverse set of shapes and broad range of applications (from household income levels to option market pricing), this type XII variation has been particularly handy for creating histograms that represent data sets accurately.
The Burr distribution Type XII offers an effective means of accurately describing a given set data. It is characterized by two shape parameters (c and k), both having positive values, as well as a scale parameter, α. While the three-parameter model allows for skew in addition to variation of mean and variance with only c,k and α being involved; when γ equals zero it also permits control over location along the x-axis – allowing you to adjust how your four dimensional picture shifts accordingly. With these features combined together into one package providing easy access that fits effectively opposing yet complementary needs such as skewness vs location adjustments – Making it simpler than ever before to get just the sort of fit needed.
The pdf for the Burr distribution (Type XII) is:
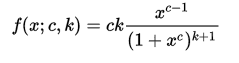
The cumulative distribution function (CDF) is:
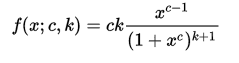
Similarity to Other Distributions
- A compounded Weibull with a gamma distribution as its shape parameter.
- The gamma distribution,
- The J-shaped beta distribution,
- The loglogistic distribution,
- The lognormal distribution,
- The normal distribution.
Other Types of Burr Distributions
- The Burr I family is the same as the uniform distribution.
- The Burr Type II distribution is the same as the generalized logistic distribution.
- The Burr Type III (also called the inverse Burr distribution or Dagum type distribution) is (along with type XII) commonly used for statistical modeling. This simple distribution is can be obtained from the PDF of the Burr type II: replace “X” in the PDF with “ln(x)” (Johnson et. al).
- Burr Type IV: usually defined by the CDF(NIST) F(x;r,c) = [1 + (c-x)/x)**(1/c)]**(-r) 0 < x < c; c, r > 0 -INF < x < INF; r, k, s > 0″>. When the location parameter (l) = 0 and scale parameter (s) = 1, it becomes the standard Burr type VI distribution.
- Burr Type X: the same as the generalized Rayleigh distribution.
- A five-parameter distribution, the beta Burr XII, is useful for modeling lifetime data.
References:
Burr, I. W. (1942). “Cumulative frequency functions”. Annals of Mathematical Statistics 13 (2): 215–232.
Feroze, N. & Aslam, M. (2013) “Maximum Likelihood Estimation of Burr Type V Distribution under Left Censored Samples.” WSEAS Transactions on Mathematics. Retrieved October 7, 2016 from here.
Johnson, N.L. et. al (1995). “Continuous Univariate Distributions“. Vol. 2, John Wiley & Sons, New York, NY, USA, 2nd edition.
Tadikamalla, Pandu R. (1980), “A Look at the Burr and Related Distributions”, International Statistical Review 48 (3): 337–344