Probability Distributions > Beta Distribution
What is a Beta Distribution?
A Beta distribution is a versatile way to represent outcomes for percentages or proportions. For example, how likely is it that a rogue candidate will win the next Presidential election? You might think the probability is 0.2. Your friend might think it’s 0.15. The beta distribution gives you a way to describe this.
One reason that this function is confusing is there are three “Betas” to contend with, and they all have different meanings:
- Beta(α, β): the name of the probability distribution.
- B(α, β ): the name of a function in the denominator of the pdf. This acts as a “normalizing constant” to ensure that the area under the curve of the pdf equals 1.
- β: the name of the second shape parameter in the pdf.
The basic beta distribution is also called the beta distribution of the first kind. Beta distribution of the second kind is another name for the beta prime distribution.
Probability Density Function
The general formula for the probability density function is:
![]()
where:
α and β are two positive shape parameters which control the shape of the distribution.
Software Options
Most software packages have options for the beta distribution.
Mathematica
Implement a beta distribution by typing BetaDistribution[alpha,beta].
R
dbeta(x, shape1, shape2, ncp = 0, log = FALSE)
pbeta(q, shape1, shape2, ncp = 0, lower.tail = TRUE, log.p = FALSE)
qbeta(p, shape1, shape2, ncp = 0, lower.tail = TRUE, log.p = FALSE)
rbeta(n, shape1, shape2, ncp = 0)
where:
- x, q = vector of quantiles.
p = vector of probabilities. - n = # of observations.
- shape1, shape2 = shape parameters α and β
- ncp = non-centrality parameter.
- log, log.p = logical; if TRUE, probabilities p are given as log(p).
- lower.tail = logical; if TRUE (default), probabilities are P[X ≤ x], otherwise, P[X > x].
Excel Beta Distribution: BETA.DIST & INV.BETA
Watch the video for an example of BETA.DIST:
The Microsoft Excel beta distribution format depends on which version of Excel you are using; Excel 2010 and later uses the BETA.DIST function, while earlier versions use BETADIST. You’ll need to know alpha and beta, both of which refer to the parameters describing the distribution. Five inputs are needed:
- The value where you want to evaluate the function.
- Alpha and Beta, the parameters of the distribution which determine shape.
- The lower and upper bound.
An extra input is needed for the Excel 2010 Beta Distribution: cumulative. Cumulative is a logical value that determines the function’s form and can either be TRUE (returns the cumulative distribution function) or FALSE (returns the probability density function).
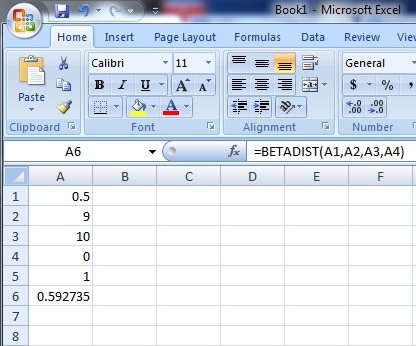
Example problem: Calculate a cumulative distribution function for a beta distribution in Excel at 0.5 with an alpha of 9, a beta of 10, a lower bound of 0 and an upper bound of 1.
Excel 2007 and Earlier:
Step 1: Type the value where you want to evaluate the function in cell A1. For this example, type “.5” in cell A1.
Step 2: Type the value for alpha in cell A2 and then type the value for beta in cell A1. For this example, type “9” in cell A2 and then type “10” in cell A3.
Step 3: Type the lower bound in cell A4 and then type the upper bound in cell A5. For this example, type “0” in cell A4 and then type “1” in cell A5.
Step 4: Type the beta distribution function into cell A6. The format of the function is =BETADIST(value,alpha,beta,lower bound,upper bound). For this example, type “=BETADIST(A1,A2,A3,A4,A5)” into cell A6. Press “Enter” to see the result for the beta distribution, which is 0.592735.
Excel 2010 and later
Step 1: Follow steps 1 through 3 in the Excel 2003-2007 section above.
Step 2: Type the beta distribution function into cell A6. The format of the function is =BETA.DIST(value,alpha,beta,cumulative,lower bound,upper bound). For this example, type “=BETA.DIST(A1,A2,A3,TRUE,A4,A5)” into cell A6. Press “Enter” to see the result for the beta distribution, which is 0.592735.
Beta Density Function
The Beta distribution is an excellent way to represent outcomes like probabilities or proportions.
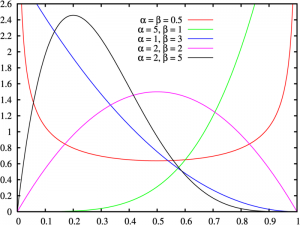
The values of α and Β determine the shape of the beta density function. For example, if α < 1 and Β < 1, the graph’s shape will be a “U” (see the red plot on the picture above, and if α = 1 and Β = 2, the graph is a straight line; If you look at the graph above, the blue line is almost a straight line: that’s because α = 1 and Β = 3.
The probability function P(x) and distribution function D(x) for the Beta Distribution are:
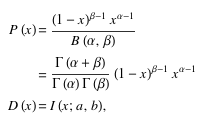
Applications of the Beta Density Function
The beta distribution is used for many applications, including Bayesian hypothesis testing, the Rule of Succession (a famous example being Pierre-Simon Laplace’s treatment of the sunrise problem), and Task duration modeling. The beta distribution is especially suited to project/planning control systems like PERT and CPM because the function is constrained by an interval with a minimum (0) and maximum (1) value.
References:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 944-945, 1972
Evans, M.; Hastings, N.; and Peacock, B. “Beta Distribution.” Ch. 5 in Statistical Distributions, 3rd ed. New York: Wiley, pp. 34-42, 2000.