Homogeneity of Variances > Bartlett’s Test
What is Bartlett’s Test?
There are actually two tests called Bartlett’s. The first part of this article is for Bartlett’s test for homogeneity of variances. If you’re looking for Bartlett’s test for sphericity (testing that the correlation matrix has an identity matrix), skip to the bottom section.
Bartlett’s test for homogeneity of variances is used to test that variances are equal for all samples. It checks that the assumption of equal variances is true before running certain statistical tests like the One-Way ANOVA. It’s used when you’re fairly certain your data comes from a normal distribution. A similar test, called Levene’s test, is a better choice for non normal distributions.
The null hypothesis for the test is that the variances are equal for all samples. In statistics terms, that’s:
H0: σ12 = σ22 = … = σk2.
The alternate hypothesis (the one you’re testing), is that the variances are not equal for one pair or more:
H0: σ12 ≠ σ22 ≠… ≠ σk2.
The test statistic is rather ugly:
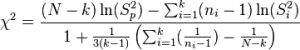
That’s why you’ll most likely want to use software for the test.
- Instructions for R.
- Excel doesn’t have a built in function, but you can download this Bartlett’s test worksheet and fill in the blanks (Worksheet downloaded from John McDonald at The University of Delaware).
- In STATA, Bartlett’s is added onto ANOVA. The basic syntax of the command is oneway dv iv where iv is a categorical variable. For more on running the test in STATA, see this Notre Dame article.
If you really want to run Bartlett’s test by hand, check out this article, which explains how to do it in great detail.
Bartlett’s Test for Sphericity
Bartlett’s test for Sphericity compares your correlation matrix (a matrix of Pearson correlations) to the identity matrix. In other words, it checks if there is a redundancy between variables that can be summarized with some factors.
- In IBM SPSS 22, you can find the test in the Descriptives menu: Analyse-> Dimension reduction-> Factor-> Descriptives-> KMO and Bartlett’s test of sphericity.
Reference:
Snedecor, George W. and Cochran, William G. (1989), Statistical Methods, Eighth Edition, Iowa State University Press.