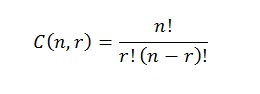Contents (Click to skip to that section):
- Definitions
- Permutation Formula
- Combinations Formula & Examples
- What if I don’t know which formula to use?
- Using technology:
- What are Derangements?
Permutation and Combination: Definition
Watch the video for an overview and examples:
A permutation or combination is a set of ordered things. The “things” can be anything at all: a list of planets, a set of numbers, or a grocery list. The list can be in a set order (like 1st, 2nd, 3rd…) or a list that doesn’t have to be in order (like the ingredients in a mixed salad). The hardest part about solving permutation and combination problems is: which is a combination and which is a permutation?
- Combination: If you don’t care what order you have things, it’s a combination. Think of combining ingredients, or musical chords: Flour, salt and water in a bowl is the same as salt, water and flour. Lottery tickets, where you pick a few numbers, are a combination. That’s because the order doesn’t matter (but the numbers you select do). You can also have combinations in mathematics, like combinations of functions or linear combinations.
- Permutation: If you do care about order, it’s a permutation. Picking winners for a first, second and third place raffle is a permutation, because the order matters. Permutation isn’t a word you use in everyday language. It’s the more complex of the two. Details matters: Eggs first? Then salt? Or flour first?
The word “combinations” has slipped into English usage for things like a “combination lock”. However, the kind of lock you put around your bicycle should (at least, from a stats point of view) be called a “permutation lock,” because the order does matter.

Use in Real Life
Why do we care about all this in real life? Combinations and permutations have hundreds (possibly, thousands) of applications, the most obvious of which is gambling:
- Lottery organizations need to know how many ways numbers can be chosen in order to calculate odds.
- Slot machine manufacturers need to know how many ways the pictures on the wheels can line up, to calculate odds and prize money.
Permutations = More Possibilities
You always have fewer combinations than permutations, and here’s why:
Take the numbers 1, 2, 3, 4. If you want to know how many ways you can select 3 items where the order doesn’t matter (and the items aren’t allowed to repeat), you can pick:
- 123
- 234
- 134
- 124
However, if you want permutations (where the order does matter, the same set has 24 different possibilities. Just take the first set of numbers listed above {1, 2, 3} and think of the ways you can order it.
- 123
- 132
- 321
- 312
- 231
- 213
There are six ways to order the numbers, which means there are 4 x 6 ways to order the set of four numbers.
Repetitions
Repetitions are just repeating numbers. They become important when it comes to choosing the right formula.
- 123 has no repetitions (each of those numbers is unique).
- 223 has the number 2 repeated.
Allowing repetition depends on your situation. For example:
- Combination locks can have any number in any position (for example, 9, 8, 9, 2), so repetitions are allowed. The number “9” appears twice here.
- Lottery numbers don’t allow repetition. The same number won’t appear twice in the same ticket. For example, you can pick numbers 67, 76, and 99. But you can’t choose 67, 67, and 67 as your winning ticket.
Logic should tell you if repetitions are allowed. For example, if you’re dealing with items that aren’t going to be replaced (like lottery balls), then you’re looking at no repetitions allowed.
Back to Top
The Formulas
Combination (C) and permutation (P) each have their own formula:
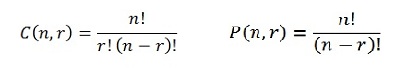
This is just multiplication and division. The “!” is the factorial symbol. That’s just a special way of multiplying numbers. To get a factorial, multiply the number by each number below it until you get to 1. For example:
4! = 4 x 3 x 2 x 1 = 24
2! = 2 x 1 = 2
Google can work out factorials for you. Type 4! into a Google search and you’ll get the answer (24).
Permutation Formulas
There are two permutation formulas. Which one you choose depends on whether you have repetitions.
For repetitions, the formula is:
- N is the number of things you are choosing from,
- r is the number of items.
For example, let’s say you are choosing 3 numbers for a combination lock that has 10 numbers (0 to 9). Your permutations would be 10r = 1,000.
For NO repetitions, the formula is:
- N is the number of things you are choosing from,
- r is the number of items.
- “!” is a factorial of a number. (See: What is a factorial of a number?)
For example, let’s say you have 16 people to pick from for a 3-person committee. The number of possible permutations is:
16! / (16 – 3)! = 16! / 13! = 3,360.
Back to Top
Combinations Formula & Examples
Example 1: 5 Choose 3
5C3 or 5 choose 3 refers to how many combinations are possible from 5 items, taken 3 at a time. What is a combination? Just the number of ways you can choose items from a list. For example, if you had a box of five different kinds of fruit and you could choose 2, you might get an apple and an orange, an orange and a pear, or a pear and an orange. But how many combinations are possible?
Watch the video for examples:
5 Choose 3: Example
Find 5C3 from Al, Betty, Charlie, Delilah, Erin.
The number of possible ways you could take 3 people from that list (Al, Betty, Charlie, Delilah, Erin) are:
- Al / Betty / Charlie,
- Al / Betty / Delilah,
- Al / Betty / Erin,
- Al / Charlie / Delilah,
- Al / Charlie / Erin,
- Al / Delilah / Erin,
- Betty / Charlie / Delilah,
- Betty / Charlie / Erin,
- Betty / Delilah / Erin,
- Charlie / Delilah / Erin.
So 5 choose 3 = 10 possible combinations.
However, there’s a shortcut to finding 5 choose 3. The combinations formula is:
nCr = n! / ((n – r)! r!)
n = the number of items.
r = how many items are taken at a time.
The ! symbol is a factorial, which is a number multiplied by all of the numbers before it. For example, 4! = 4 x 3 x 2 x 1 = 24 and 3! = 3 x 2 x 1 = 6.
So for 5C3, the formula becomes:
nCr = 5!/ (5 – 3)! 3!
nCr = 5!/ 2! 3!
nCr = (5 * 4 * 3 * 2 *1) / (2 * 1)(3 * 2 * 1)
nCr = 120 / (2 * 6)
nCr = 120 / 12
nCr = 10
Note: although the C in “5c3” is often written as “choose,” it actually means Combination!
Example 2: 4 choose 2
Question: How many different combinations do you get if you have 4 items and choose 2?
Answer: Insert the given numbers into the combinations equation and solve. “n” is the number of items that are in the set (4 in this example); “r” is the number of items you’re choosing (2 in this example):
C(n,r) = n! / r! (n – r)!
= 4! / 2! (4 – 2)!
= 4! /2! * 2!
= 4 x 3 x 2 x 1 / 2 x 1 * 2 x 1
= 24 / 4
= 6
The solution is 6. Here’s the full list of possible combinations:
- {1, 2}
- {1, 3}
- {1, 4}
- {2, 3}
- {2, 4}
- {3, 4}
Note: {1, 1}, {2, 2}, {3, 3} and {4, 4} aren’t included in the list, because with combinations you can’t choose the same item twice for the same set.
Example 3: 4 choose 3
How many different combinations do you get if you have 4 items and choose 3?
Answer: Insert the given numbers into the combinations equation and solve. “n” is the number of items that are in the set (4 in this example); “r” is the number of items you’re choosing (3 in this example):
C(n,r) = n! / r! (n – r)! =
= 4! / 3! (4 – 3)!
= 4 x 3 x 2 x 1 / 3 x 2 x 1 x 1
= 24 / 6
= 4
The solution is 4. The possible combinations are:
- {1, 2, 3}
- {1, 2, 4}
- {1, 3, 4}
- {2, 3, 4}
Note: Sets like {1,1,2) or {3,3,3} aren’t included in the calculation, as you can’t choose an item more than once for a set.
Example 4: 4 choose 0
4 Choose 0 is 1.
Why? This might seem like a mind bender; how can you choose none and still get 1? But you have to look at it a slightly different way.
Combinations are just the full spread of different ways you can arrange the various subsets of one larger set. For a simple example take the set of A={1,2}. You can form four subsets of this set: {}, {1}, {2}, and {1,2}. These subsets are called the combinations of set A.
If you have 4 items and you’re not choosing any, you still have those four items in the set: {1, 2, 3, 4}. In other words, you didn’t take any away, so you still have them all, i.e. 1 set.
Back to Top
What if I don’t know which formula to use?
Most of the time, you aren’t told whether you should use the permutation formula or the combination formula. Part of problem solving involves figuring this out on your own. The following examples show you how to do this.
Example problem #1: Five bingo numbers are being picked from a ball containing 100 bingo numbers. How many possible ways are there for picking different numbers?
Step 1: Figure out if you have permutations or combinations. Order doesn’t matter in Bingo. Or for that matter, most lottery games. As order doesn’t matter, it’s a combination.
Step 2: Put your numbers into the formula. The number of items (Bingo numbers) is “n.” And “k” is the number of items you want to put in order. You have 100 Bingo numbers and are picking 5 at a time, so:
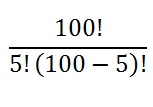
Step 3: Solve:
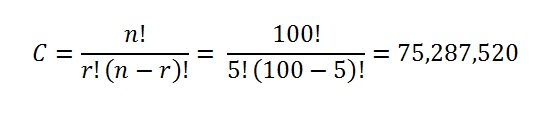
That’s it!
Example problem #2. Five people are being selected for president, vice president, CEO, and secretary. The president will be chosen first, followed by the other three positions. How many different ways can the positions be filled?
Step 1: Figure out if you have permutations or combinations. You can’t just throw people into these positions; They are selected in a particular order for particular jobs. Therefore, it’s a permutations problem.
Step 2: Put your numbers into the formula. There are five people who you can put on the committee. Only four positions are available. Therefore “n” (the number of items you have to choose from) is 5, and “k” (the number of available slots) is 4:
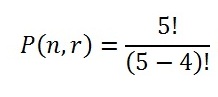
Step 3: Solve:
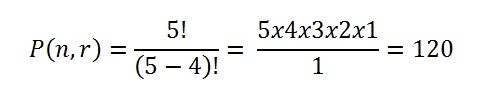
That’s it!
Calculator Tips
You have a couple of options on the internet.
- Google will evaluate factorials. Type 5! into Google search and it will give you 120 as an answer on the Google calculator.
- Use our online combinations calculator. It not only gives you the result — it gives you the working out too!
Permutations and Combinations in Excel
Permutations formula: PERMUT(number, number_chosen)
For example, if you had 100 items and wanted to choose 4, you would type the following into a blank cell:
=PERMUT(100,4)
Combinations formula: COMBIN(number, number_chosen)
For example, if you had 99 items and wanted to choose 10, you would type the following into a blank cell:
-COMBIN(99,10)
TI-83
TI 83 Combinations (n! / (n – r!) r!)
Watch the video for an example:
Example problem: If there are 5 people, Barb, Sue, Jan, Jim, and Rob, and only three will be chosen for the new Parent Teacher Association, how many combinations are possible for the committee?
Step 1: Enter the number of items on the home screen (the main input area) that you have to choose from. In the above example, you have 5 people, so press 5.
Step 2: Press the Math button.
Step 3: Use the right arrow key to tab across to “PRB”.
Step 4: Press 3. This inserts nCr onto the home screen.
Step 5: Enter the number of items you want to choose. In the above example, you want to choose 3, so press 3.
Step 6: Press ENTER. The calculator will return the result: 10.
TI 83 Permutations (n! / (n – r!))
Watch the video for an example:
Example problem: If there are 5 people, Barb, Sue, Jan, Jim, and Rob, and three will be chosen for the new Parent Teacher Association. The first person picked will be the president, then the vice president, then the secretary. How many permutations are possible for the committee?
Step 1: Enter the number of items on the home screen (the main input area) that you have to choose from. In the above example, you have 5 people, so press 5.
Step 2: Press the Math button.
Step 3: Use the right arrow button to tab across to “PRB“.
Step 4: Press 2. This inserts nPr onto the home screen.
Step 5: Enter the number of items you want to choose. In the above example, you want to choose 3, so press 3.
Step 6: Press ENTER. The calculator will return the result: 60.
Lost your guidebook? Download a new one here at the TI website.
TI-89
TI 89 Combinations: Steps:
Example problem: If there are 5 people, Barb, Sue, Jan, Jim, and Rob, and only three will be chosen for the new Parent Teacher Association, how many combinations are possible for the committee?
Step 1: Press the HOME screen on the calculator.
Step 2: Press the CATALOG key.
Step 3: Press ALPHA 6. This selects the letter “n” and brings you to the “n”s in the list. If it doesn’t, try pressing ALPHA 6 again.
Step 4: Find nCr(. Press ENTER.
Step 5: Press 5. This is the number of possible people, or n.
Step 6: Press the comma, then 3. This is the number of people we need to choose, or r.
Step 7: Press ). The entry on your calculator should now read nCr(5,3). Press ENTER. This returns you result. There are 10 possible ways this committee can be chosen.
Tip: Instead of hitting the ALPHA and 6 keys, use the scroll button to scroll through the menu.
Tip: Want to check your answer? Use our free, online combinations calculator and permutations calculator to check your work.
Derangements: Definition.
Derangements are permutations in which no object is returned to its original, right, or natural place. They are sometimes called complete permutations or rencontres numbers.
Another way of saying this is that a derangement is a permutation without fixed points. π(i) ≠ i for every i being permutated, where:
- π is the permutation,
- i is the objects being acted upon.
Note: Pi is fairly standard notation for permutations; any Greek letter is fair game, but in general pi is the one chosen across the board.
- There is no derangement possible for a set with one element; The set {a} cannot be written any other way.
- A set with two elements has just one derangement. For example, the derangement of {a, b} is {b, a}.
- For a set with three elements, there are two possible derangements. (If your set is {a, b, c}, then {b, c, a} and {c, a, b} are the two possibilities.
Formula
The number of permutations of a set of n elements is given by n! (n factorial, or n · (n-1) · (n-2)…(1)). The number of derangements of a set of n elements, which we write Dn, is given by
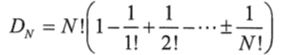
This looks long and complicated, but a little calculus can reduce it to an equation that is very, very easy to use:
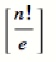
Where:
- The square bracket, [ ], is the ‘nearest integer function‘, a function which rounds whatever is inside the brackets to the nearest integer.
- “e” is Euler’s number.
The number of derangements is sometimes also written as !n, and then is called the subfactorial.
Examples of Derangements Problems
The formula above allows us to solve more involved questions like, “Six students placed their phones in one bag and then all grabbed one out randomly. What is the likelihood that no one would get his own phone?”
The number of possible permutations in this case is 6!, or 6 · 5 · 4 · 3 · 2 · 1= 720. The number of possible derangements is [6!/e], or 265. So the probability that no one would get their own phone is 265/720, or 36 percent.
Check out our Youtube channel for more stats tips! More videos added every week. Subscribe for updates. Comments always welcome.
References
“Klein, G. (2013). The Cartoon Introduction to Statistics. Hill & Wamg”
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education
Wheelan, C. (2014). Naked Statistics. W. W. Norton & Company